BIENVENIDO, Invitado ( IdentifÃcate | Registrase )
 Sep 13 2007, 03:05 PM Sep 13 2007, 03:05 PM
Publicado:
#1
|
|
|
Advanced Member    Grupo: Members Mensajes: 1.274 Desde: 11-March 08 De: Catalunya Usuario No.: 338 |
Hola Pico,
te respondo rápidamente porque voy justo de tiempo, supongo que alguien te ampliará la respuesta. En términos generales, cuánto más peso más lento se pasa por una curva. Sí es cierto que se necesita cierto peso para que los neumáticos tengan agarre mecánico, pero este peso también aumenta la inercia hacia el exterior de la curva, lo cual limita mucho la velocidad. Por eso son tan interesantes los alerones y los difusores, ya que aumentan la carga aerodinámica (aumentando por tanto el agarre) sin aumentar la masa del vehículo y por tanto sin contribuir a aumentar la inercia hacia el exterior de la curva. Esta explicación es un poco por encima y sin ser muy rigurosa, a ver si alguien lo explica en términos más científicos. Saludos!! Ozzman "If you can''t run with the big dogs, stay on the porch" |
|
|
|
 |
Respuestas
 Sep 14 2007, 01:41 AM Sep 14 2007, 01:41 AM
Publicado:
#2
|
|
|
Pilotillo    Grupo: Members Mensajes: 2.189 Desde: 11-March 08 De: Spain Usuario No.: 3.072 |
Ahí tienes la prueba, lo que te dice APR, ¿cuando marcan las vueltas rápidas?
¿Cuando salen tras repostar o cuando van con el deposito vació? El Formula 1 va rápido cuando tiene una carga aerodinamica, suficiente para pasar rápido por la curva sin perder mucha velocidad en el resto del circuito. Circuito de Indianapolis, USA. La curva peraltada del circuito es la más rápida del mundial, pero, en el "infield", pierden fiabilidad de conducción, por tanto, tienen que buscar la suficiente velocidad para la oval y la suficiente carga aerodinamica para poder trazar las curvas del infield rapidas. Aquí tendríamos que aplicar la formula de la fuerza centrifuga, para ver que el peso es directamente proporcional a el aumento de la fuerza centrifuga( tendencia a salir recto en la curva) Primero, consideramos el vehículo como una partícula. Luego, estudiamos la estabilidad de un vehículo con unas determinadas dimensiones y con una determinada distribución de carga. Curva sin peralte Un automóvil describe una trayectoria circular de radio R con velocidad constante v. Una de las principales dificultades que se presenta a la hora de resolver este problema es la de separar el movimiento tangencial (uniforme con velocidad constante) del movimiento radial del vehículo que es el que trataremos de estudiar. Fundamentos físicos Suponemos que el vehículo describe una trayectoria circular de radio R con velocidad constante v. Para un observador inercial, situado fuera del vehículo, las fuerzas que actúan sobre el móvil son: * el peso * la reacción de la carretera * la fuerza de rozamiento. Esta última, es la que hace que el vehículo describa una trayectoria circular. Como hay equilibrio en sentido vertical la reacción del plano es igual al peso N=mg Aplicando la segunda ley de Newton al movimiento en la dirección radial 
Siendo v la velocidad del móvil y R el radio de la circunferencia que describe A medida que se incrementa la velocidad v, se incrementa la fuerza de rozamiento Fr hasta que alcanza un valor máximo dado por el producto del coeficiente de rozamiento estático por la reacción del plano, m N. La velocidad máxima v que puede alcanzar el vehículo para que describa una curva circular de radio R es, por tanto 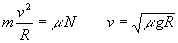
Como podemos apreciar en el programa interactivo, a medida que se aumenta la velocidad del móvil, la fuerza de rozamiento crece hasta alcanzar el valor máximo m N, la trayectoria del vehículo es una circunferencia. Si la velocidad del móvil es superior a la máxima, la fuerza de rozamiento, que es perpendicular al vector velocidad, tiene un valor constante e igual a su valor máximo, la trayectoria del móvil deja de ser circular. Para simplificar el problema hemos supuesto que los coeficientes de rozamiento estático y cinético tienen el mismo valor. http://www.sc.ehu.es/sbweb/fisica/dinamica/circular/din_circular.htm[URL-NOMBRE]Fuerza centrifuga, dicese la que te escupe de la carretera y te das el tortazo Edited by - Vincent Hill on 13/09/2007 20:59:41 |
|
|
|
Mensajes en este tema
 Ozzman duda de la fisica de un coche Sep 13 2007, 03:05 PM
Ozzman duda de la fisica de un coche Sep 13 2007, 03:05 PM
 pico Muchas gracias por tu respuesta de todas formas a ... Sep 13 2007, 05:35 PM
pico Muchas gracias por tu respuesta de todas formas a ... Sep 13 2007, 05:35 PM
 KIT El peso no ejerce provoca más rapidez, a mas ... Sep 13 2007, 07:03 PM
KIT El peso no ejerce provoca más rapidez, a mas ... Sep 13 2007, 07:03 PM
 APR básicamente, Cuándo va más ráp... Sep 13 2007, 09:01 PM
APR básicamente, Cuándo va más ráp... Sep 13 2007, 09:01 PM
 pico gracias VINCENT HILL, la cuestion es que segun las... Sep 14 2007, 03:27 AM
pico gracias VINCENT HILL, la cuestion es que segun las... Sep 14 2007, 03:27 AM
 Vincent Hill La verdad, analizando estas formulas, realmente se... Sep 14 2007, 03:51 AM
Vincent Hill La verdad, analizando estas formulas, realmente se... Sep 14 2007, 03:51 AM
 marroba Holas, creo que hay un error.
Hasta: m*v2/r=coef*... Sep 14 2007, 04:31 AM
marroba Holas, creo que hay un error.
Hasta: m*v2/r=coef*... Sep 14 2007, 04:31 AM
 pico Marroba creo q has dado en el clavo.
La conclusion... Sep 14 2007, 05:06 AM
pico Marroba creo q has dado en el clavo.
La conclusion... Sep 14 2007, 05:06 AM
 marroba >básicamente, Cuándo va más r... Sep 14 2007, 06:30 AM
marroba >básicamente, Cuándo va más r... Sep 14 2007, 06:30 AM
 ejquesemeinercia hola a toos,
me busta el tema este anque entender... Sep 14 2007, 02:57 PM
ejquesemeinercia hola a toos,
me busta el tema este anque entender... Sep 14 2007, 02:57 PM
 _Erredege_ ¿Este último mensaje es de coña no? Sep 14 2007, 05:32 PM
_Erredege_ ¿Este último mensaje es de coña no? Sep 14 2007, 05:32 PM
 calimbaire no sé si va de coña o en serio... pero y... Sep 14 2007, 08:33 PM
calimbaire no sé si va de coña o en serio... pero y... Sep 14 2007, 08:33 PM
 calimbaire ah... y una duda, Marroba, donde dices fuerza cent... Sep 14 2007, 09:22 PM
calimbaire ah... y una duda, Marroba, donde dices fuerza cent... Sep 14 2007, 09:22 PM
 Vincent Hill MARROBA
Gracias, busque y copie, en esa pagina se ... Sep 15 2007, 12:19 AM
Vincent Hill MARROBA
Gracias, busque y copie, en esa pagina se ... Sep 15 2007, 12:19 AM
 dvn2o jajaja, me ha gustado mucho ese de la gasolina y l... Sep 15 2007, 07:25 AM
dvn2o jajaja, me ha gustado mucho ese de la gasolina y l... Sep 15 2007, 07:25 AM
 ejquesemeinercia no,no que va en serio, que yo no pretnedo ser grac... Sep 15 2007, 01:04 PM
ejquesemeinercia no,no que va en serio, que yo no pretnedo ser grac... Sep 15 2007, 01:04 PM
 ejquesemeinercia VincentHill perdona igual no se me ha entendido pe... Sep 15 2007, 01:11 PM
ejquesemeinercia VincentHill perdona igual no se me ha entendido pe... Sep 15 2007, 01:11 PM
 ejquesemeinercia perdon que sea pesada pero el assunto es que me in... Sep 15 2007, 01:25 PM
ejquesemeinercia perdon que sea pesada pero el assunto es que me in... Sep 15 2007, 01:25 PM
 Vincent Hill El peso del combustible, afecta normalmente para m... Sep 15 2007, 03:28 PM
Vincent Hill El peso del combustible, afecta normalmente para m... Sep 15 2007, 03:28 PM
 ejquesemeinercia gracias Vincenjill, me has aclarado un monton con ... Sep 15 2007, 03:36 PM
ejquesemeinercia gracias Vincenjill, me has aclarado un monton con ... Sep 15 2007, 03:36 PM
 Vincent Hill Se ha hecho lo que se ha podido, esto seria un afo... Sep 15 2007, 04:15 PM
Vincent Hill Se ha hecho lo que se ha podido, esto seria un afo... Sep 15 2007, 04:15 PM
 pico joe cuanto sabes vicent hill, eres todo un erudito... Sep 15 2007, 06:46 PM
pico joe cuanto sabes vicent hill, eres todo un erudito... Sep 15 2007, 06:46 PM
 marroba A ver...
-Sobre la gasolina arriba y abajo:
a) S... Sep 15 2007, 07:25 PM
marroba A ver...
-Sobre la gasolina arriba y abajo:
a) S... Sep 15 2007, 07:25 PM
 pico Un saludo a todo el mundo... Lo cierto es q tengo ... Sep 13 2007, 05:11 AM
pico Un saludo a todo el mundo... Lo cierto es q tengo ... Sep 13 2007, 05:11 AM   |
1 usuario(s) está(n) leyendo este tema (1 invitado(s) y 0 usuario(s) anónimo(s))
0 usuarios(s) registrado(s):
| Fecha y Hora Actual: 15th October 2025 - 05:14 AM |